Method for determining the spatial position of the center of gravity of machines

Introduction

It is hard to overestimate the role of a precise and convenient method for determining the position of the center of gravity of manufactured products. The position of the center of gravity of a machine impacts such qualitative characteristics as trave­ling stability, buoyancy, distribution of load among supporting structures, smooth travel, etc. [1].

Fig. 1. Measurement diagram: 1 - tested machine; 2 - brackets; 3 - slings; 4 - cross-beam; 5 - dynamometers

The simplest and most common (applied, among others, by JSC lEMZ “Kupol”) experimen­tal method for determining the center of gravity of a machine is as follows. The tested machine (Pos. 1 in Fig. 1) is hung up using special brackets (Pos. 2) and slings (Pos. 3) attached to the cross-beam (Pos. 4). The cross-beam is lifted up using the crane beam. The center of gravity position in the uplifted position impacts sling load distribution. The coordinates of the center of gravity of a ma­chine x_c, y_c are determined based on dynamo­meter (Pos. 5) readings using the equations of equilibrium for the hung-up machine:

T_i - sling tension load i.

This method has certain disadvantages, the most significant of which is impossibility to de­termine the elevation of the center of gravity z_c.

An alternative method for determining the center of gravity is specified in [2]. According to GOST 30750 -2001, the center of gravity is deter­mined by measuring the reactions at the supports when installing the tested machine in horizontal and two tilted positions: with either front or rear part lifted, as shown in Fig. 2. To determine the reactions at the supports, the platform weighing scale is used.

Fig. 2. Diagrams to the method as per GOST 30750 -2001: а - first weighing; b - second weighing; c - third weighing

The first weighing is performed with the body tilted in the longitudinal plane at angle a (Fig. 2, a). The tilt is ensured through lifting of the machine front part using the crane beam. The weighing results allow to determine the coordinate of the center of gravity a_c by the formula

For the second weighing, the machine is tilted β to the opposite side in the same plane, through lifting the machine rear part (Fig. 2, b). The second coordinate of the center of gravity b_c is determined by the formula

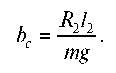
Points in plane Ω correspond to this coor­dinate.

The first two weighings limit the search region for the center of gravity to straight line h in the intersection of planes Θ and Ω. The exact position of the center of gravity on straight line h is determined by coordinate X_c, calculated by the formula

depending on the results of third weighing with the machine being in the horizontal position (Fig. 2, c). To determine the product actual mass m, one more weighing is required.

The standard method has an obvious ad­vantage over the method applied at the enter­prise due to the possibility of determining the elevation of the center of gravity, however, it requires platform weighing scale, increased number of weighings and it is more time con­suming.

Among existing engineering solutions for determining the products center of gravity there is no method that would be simple and universal enough, as well as provide com­prehensive information on the position of the center of gravity without increasing the amount of production equipment required for obtaining the same. Considering the above, the objective of this article is to develop a method for determining the spatial position of the center of gravity through hanging up using simple and widespread process means and subject to minimizing the use of special force-measuring instruments and the number of weighing operations.

For completing the experimental part of the process, we will forgo using special complex rigging in favor of load carrying one available in the shops: load cross-beam, slings and either frame crane or tower crane will be used. In this case, the objective can be achieved through estimating analytical relationships be­tween the positions of a product hung up on the load cross-beam in the equilibrium condition and three coordinates of its center of gravity. The relationships can be expressed with the equations of equilibrium of the measuring sys­tem elements and analytic geometry equa­tions, and their quantity and composition in a mathematical model can be chosen in such a way as to exclude force parameters from the list of independent variables (subject to experi­mental determination). This will allow to ex­clude the necessity of using force-measuring instruments as part of the measuring circuit.

Depending on the number of simulta­neously processed coordinates, the considered problem may either be spatial or plane. The practical interest is the solution of the most common spatial problem. However, using the proposed method, it would be efficient to per­form a preliminary abstract check of a prin­cipal possibility to determine the most prob­lematic elevation coordinate by the example of solving the plane problem simple in mathe­matical terms.

Plane problem solution

Steady equilibrium condition of substatic sys­tem “cross-beam - slings - machine” depends on the coordinates of the center of gravi­ty of the machine and the cross-beam. Two unknown coordinates of the machine center of mass can be determined similarly with the con­sidered standard method, through hanging up the machine at two different angles. Hanging at different angles can be done through using pairs of slings of different length, while inter­changing the pairs.

A combination of system “cross-beam - slings - machine” positions corresponds to every position of the center of gravity before and after interchanging the slings position. In order to provide analytical representation of this correspondence, let us refer to the sys­tem elements loading diagram for two cases shown in Fig. 3. Here, ADG - cross-beam hinge-mounted relative to the hanger with a single degree of freedom - rotation around hinge D. The position of the cross-beam is de­fined by angle γ_Ti, where i ∈{ ,1 2} - sequence number of hanging operation. The cross-beam is characterized by the following known pa­rameters: mass m_T, dimensions H_T and l_T, position coordinates of its center of mass Z_CT. AO and GK - slings with lengths l₁ and l₂ , re­spectively. Sling tension loads T_yi and T_2i are deflected from the vertical by angles α_1i and α_2i, respectively.

Fig. 3. Calculation patterns for plane problem: а - before interchanging the sling pairs position; b - after interchanging the sling pairs position

The tested machine is conventionally shown as rectangle MNFE. Points O and K - slings fastening to the machine body (brackets). Point С - the machine center of gravity with unknown coordinates x_c, z_c relative to left bracket O in the machine coordinate system. Polar coordinates of the machine center of gravity - polar distance ρ and its tilt angle φ. The machine orientation in steady position i is defined by its angle of tilt with the horizon­tal γ_i. Other known machine parameters: mass n, dimensions L_M and H, distance between brackets L, coordinate of the left bracket rela­tive to the machine edge L_O.

In the figure plane, we shall accept Car­tesian coordinates xDz. We shall assume slings connections with the machine and the cross­beam to be perfect frictionless hinges, ignoring slings elongation under tension and slings mass.

Let us relate the system positions at two hanging operations with Cartesian coordinates of the machine center of gravity using the equations of equilibrium [3]. In steady position i, the resultant moment created by the machine and cross-beam gravity forces shifted relative to point D shall be zero:

where AD - length of cross-beam arm, AD = 

δ- angle at tops A and G of the cross­beam, ;

γ₁ and γ₂ - angles of machine tilt relative to the horizontal in the first case and second case, respectively; upper sign «+» is applicable to γ₁, lower «-» to γ₂.

Joint solution of two equations (1), compiled for each of two cases subject to known parameters of the system position (Y_Т1, Y_Т2, Y₁, Y₂, ^α₁₁, ^α₂₂), allows to determine polar coordinates of the machine center of gravity ρ and φ. Conversion to Cartesian co­ordinates of the center of gravity can be done using the known method [4]:

Parameters γ_Т1, γ_Т2, γ₁, γ₂, α₁₁, α₂₂ are predetermined based on mathematical models describing each of two equilibrium positions of the system. The models contain the equations of equilibrium and equations expressing geome­trical constraints of the system elements. Two force equations and one moment equation of cross-beam equilibrium are as follows

where tension force of hauling cable is defined by the formula

T = (m + m_T) g.                                                         (6)

Geometrical equations express closedness of substatic tetragon AGKO:

In projections on axis z and x we will obtain two more equations

Thus, five equations are obtained for each case i with six variables: T_1i,T_2i, α_1i, α_2i, γ_Ti, γ_i.. One of these variables can be considered independent and subject to measurement. The remaining five variables are defined depending on the same and using five obtained equations.

If geometrical variable, for example ma­chine tilt angle Y i, is chosen as an independ­ent variable, there will be no need to define force variables and, consequently, use force­measuring instruments. It is quite simple to de­fine the tilt angle experimentally, for example, by the difference in elevation of two points of the machine: E and F above the floor level by the formula

Thus, we have ascertained the principal possibility to determine the center of gravity elevation coordinate through hanging up and the absence of the need to use any force­measuring instruments for this purpose.

As the second step, let us solve the spa­tial problem and develop an algorithm for de­termining the position of the center of gravity.

Spatial problem solution

The spatial problem solution is very similar to the plane problem solution. The main dif­ferences are in the increased number of pa­rameters describing equilibrium conditions of the measuring system elements, which are defined by a large number of jointly solved equations.

When solving the spatial problem, it is convenient to use matrix formulas at spatial turns and shifts [4]. Thus, spatial objects will be set as the coordinate matrices of their nodal points. Spatial forces are defined by three inde­pendent parameters. They shall be set as pro­jections on the coordinate axis, thus allowing to use the corresponding coordinates of these forces application points as moment arms in the static equations.

Calculation patterns of the system in space for two weighings are shown in Fig. 4. The position of the cross-beam ABDEF in case i is set by the angles of its rotation around own coordinate axes γ_Tix, γ_Tiy and γ_Tiz, n_A - vector of normal to the plane of figure BDEF. T_jik - projections of sling tension force j in case i to coordinate axis k.

Fig. 4 (beginning). Calculation patterns for spatial problem: а - before interchanging the sling pairs position

Fig. 4 (ending). Calculation patterns for spatial problem: b - after interchanging the sling pairs position

If the matrix of spatial coordinates of the cross-beam nodal points prior to its rotation around own axes passing through hinge А is as follows

then, in steady equilibrium condition, the coordi­nates of nodal points depend on the angles of cross­beam orientation γ_Tiy and γ_Tiz in accordance with the known formula

The coordinates of sling ends are connected with the coordinates of cross-beam nodal points with the equation

where T_ij - sling tension loads, T_ij = 

BO, DG, FM, EK - length of slings elongated under tension.

According to Hooke’s law, sling length j in elongated condition - l_j + Jl_jT_ji,, where J - lengthwise sling elasticity [5].

The coordinates of nodal points provided in equations (10) and (11) are used in mathe­matical models of system position in two cases.

The mathematical models represent a complex of equilibrium equations and geomet­rical equations. Six cross-beam equilibrium equations for case i are as follows

where T - tension force of hauling cable, defined by the formula (6);

m B ∈ (B, E, F, D), - dependencies of the nodal points coordinates on the cross-beam orientation angles, calculated by the formula (10).

Geometrical equations express the condition of closedness of substatic tetragons BOKE and BOMF at different machine spatial orientation γ_iy и γ_iz:

In the projections on the coordinate axes considering (10) and (11), we will additionally get nine equations:

Subject to known machine orienta­tion angles, the system of fifteen equations (12) - (26) solved relative to 15 variables - T_1ix , T_1iy , T_1iz, T_2ix , T_2iy , T_2iz, T_3ix , T_3iy , T_3iz, T_4ix , T_4iy , T_4iz, γ_Tix , γ_Tiy , γ_Tiz - allows to complete­ly define the parameters of system position in this case i.

The angles of machine spatial orientation γ_ix , γ_iy and γ_iz in case i are calculated based on matrix transformation of the coordinates of three points V, Q, R at machine rotation (see Fig. 4):

If based on formula (21) we express the dif­ferences between elevation coordinates of points V, Q, R pairwise and equate them with the differ­ences between measured elevation of these points above the floor level, we will obtain a system of three equations for defining angles 

The parameters of system position in two cases are required for defining the coordinates of the machine center of gravity based on moment equations of equilibrium

where functional dependencies of the machine center of gravity coordinates in system xyz on the coordinates of the center of gravity in own coordinate system X_C, Y_C, Z_C:

functional dependencies of the cross-beam nodal points coordinates on its orientation angles  are expressed based on the formu­la (10).

Through solving equations (29) relative to X_C, Y_C, Z_C, we define the unknown position of the ma­chine center of gravity.

Thus, subject to known parameters of measur - m, m_T , Z_cT , H_T ,a_T , b_T , L, L_M , L_O, B, l₁, l₂, l₃, l₄, J - the algorithm of defining the machine center of gravity in space includes the following steps:

1. hang up the system (see Fig. 4, a) and wait until equilibrium settles;
2. measure the elevation of three points of the machine h_V1, hQ₁, h_R1 above the floor level;
3. solve the system of equations (12) - (26), having accepted i = 1 relative to T_11x, T_11y, T_11z, T_21x, T_21y , T_21z, T_31x , T_31y , T_31z, T_41x , T_41y , T_41z, γ_{T x1} , γ_{T y1} , γ_T1z^;
4. interchange the positions of the pairs of slings 1, 2 and 3, 4 (see Fig. 4), hang up the system and wait until equilibrium settles;
5. define the elevation of the machine points h_V2, h_Q2, h_R2 above the floor level;
6. solve the system of equations (12) - (26), having accepted i = 2 relative to T_12x , T_{12 y} , T_12z, T_22x , T_{22 y} , T_22z, T_32x , T_{32 y} , T_32z, T_42x , T_{42 y} , T_42z, γ_{T x 2} , γ_{T y 2} , γ_{T 2z}^;
7. solve the system of equations (28) for each of two cases of hanging up and define angles y_1x y_1y y_1z y_2x y_2y y_2z;
8. use the parameters calculated as per item 3, 6, 7 for solving the system of equa­tions (29) relative to the coordinates of the ma­chine center of gravity in own coordinate sys­tem X_c ,Y_c, Z_c.

The program was written in MathCAD to reduce labour intensity connected with mathe­matical processing of the measurement results. The advantages of using MathCAD for solving this problem are based on the built-in tools for solving non-linear equation systems.

The developed program allows automatic calculation of the coordinates of the machine center of gravity depending on the parameters of the measuring system and depending on the measured elevations of the machine points V, Q, R above the floor level for two cases of hanging. The program outputs numeric values of the coordinates and shows the positions of measuring system with the elements’ centers of gravity in three projections for each case, as well as the machine center of gravity in own coordinate system in three projections. The examples of the program operation results are shown in Fig. 5.

Conclusion

The developed method of determining the co­ordinates of the center of gravity of a machine does not require use of force-measuring in­struments as part of the measuring circuit, is targeted at using simple hanging up facilities available in the shop, allows to determine all three coordinates of the center of gravity and is a good alternative for the method used at the enterprise.

The program written based on the deve­loped algorithm allows to reduce labour inten­sity connected with mathematical processing of the measurement results.

This article provides a consideration of a principal possibility to determine the center of gravity using the proposed method, based on mathematical processing. Within the framework of further works, the accuracy of the method will be assessed, the effect of errors of the ap­plied means on the error of the center of gravity determination will be studied, the results of pi­lot testing carried out at the JSC IEMZ “Kupol” production facilities will be provided.